1.9.4. Méthodes de discrétisation#
Pour rappel, le but d’une méthode de mise en classe est de transformer une variable numérique continue en groupes discrets. La discrétisation a deux objectifs principaux:
Séparer les valeurs de manière à ce que les entités semblables sont regroupées, et les entités sans ressemblance se retrouvent dans des classes différentes.
Dans la mesure du possible, les caractéristiques de la distribution statistique des valeurs sont maintenues.
Différentes méthodes de discrétisations ont été proposées et qui permettent de respecter ces critères plus ou moins bien. Nous allons voir ci-dessous quelques-unes de ces méthodes pour ensuite discuter leur utilisation. Nous allons aussi faire une comparaison avec des méthodes statistiques qui poursuivent un but similaire.
1.9.4.1. Méthode des seuils naturels#
La méthode des seuils naturels, appelée aussi la méthode des seuils observés, découpe une série de valeurs sur la base de ruptures identifiées de manière visuelle à partir d’un graphique. Le but est de trouver les écarts(= seuils) les plus grands qui sont utilisés comme limites de classes.
Concrètement, on copie les valeurs dans un logiciel comme Excel ou LibreOffice Calc. Ensuite, il faut trier les valeurs et faire un graphique des valeurs:
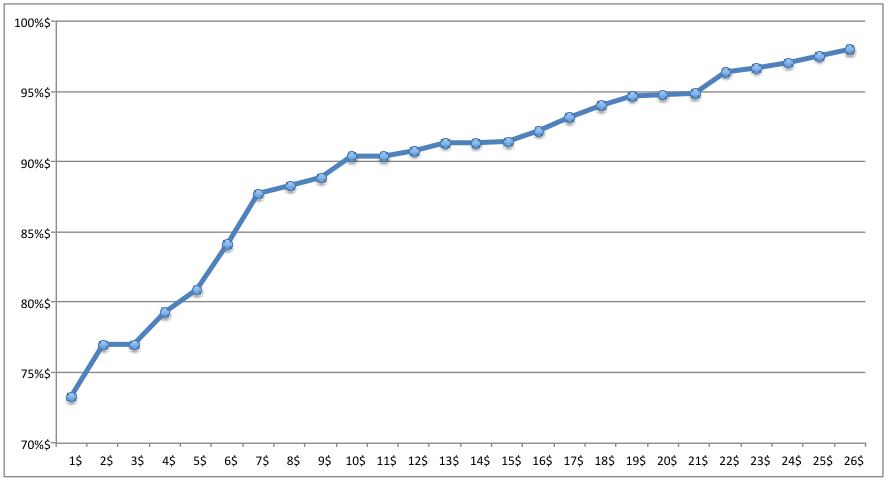
Ensuite, on identifie de manière visuelle les “sauts” dans ce graphique:
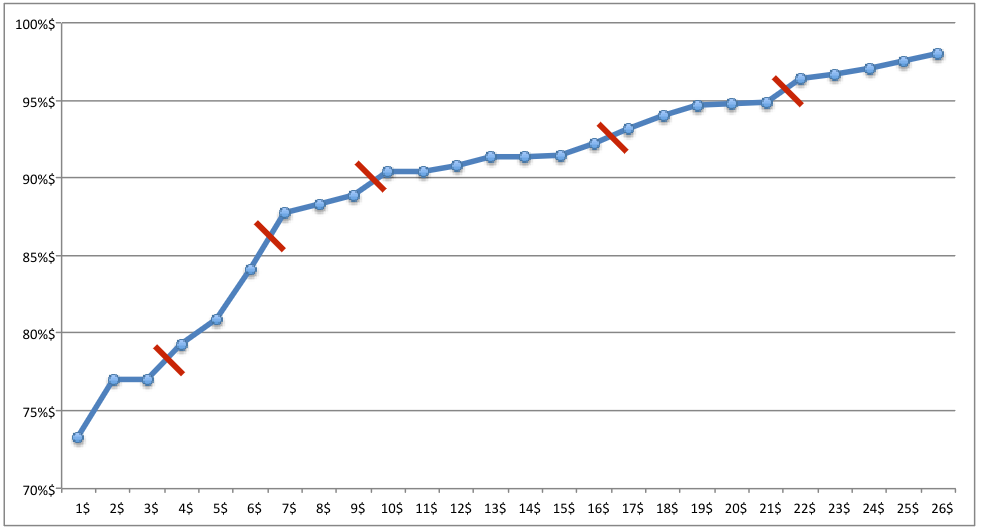
En plus d’identifier les sauts, on va essayer de répartir les classes de manière plus ou moins homogène. On va aussi essayer d’éviter des classes avec une seule observation, sauf suivant comment aux extrémités pour tenir compte des cas spéciaux.
La méthode des seuils naturels permet en même temps de trouver un nombre optimal de classes.
L’idée de la méthode des seuils naturels est de regrouper les valeurs semblables. Ainsi, si on a une suite de valeurs comme la suivante:
| 4,9 | 4,95 | 4,98 | 5,01 | 5,47 | 5,48 |
la méthode des seuils naturels va éviter de proposer une limite de classe entre les valeurs 4,98 et 5,01 (écart de 0,03), mai plutôt entre 5,01 et 5,47 (écart de 0,46). Sur un graphique, les valeurs ci-dessus se présentent comme suit:
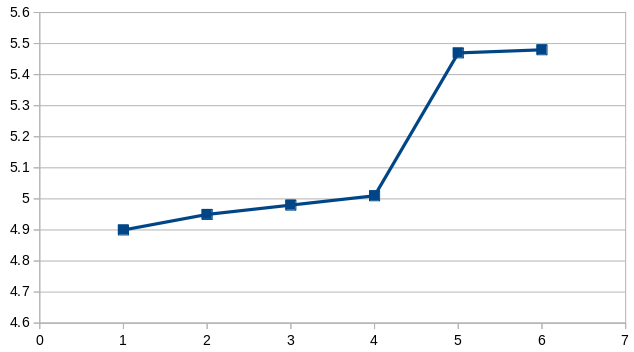
Le seuil entre 5,01 et 5,47 est très bien visible.
1.9.4.2. Méthode des effectifs égaux#
La méthode des effectifs égaux est aussi appelée méthode des quantiles. Elle se base sur une série de percentiles définies. Généralement, on choisit entre trois variantes selon le nombre de classes:
avec une discrétisation en 4 classes, on choisit les quartiles comme limites de classes.
avec 5 classes, on choisit les 2ème, 4ème, 6ème et 8ème déciles comme limites de classes.
avec 6 classes, on choisit le 1er décile, les quartiles et le 9ème décile comme limites de classes.
Dans le cas de 4 ou 5 classes, le nombre d’entités géographiques dans chaque classe est donc approximativement égal (le nombre peut varier légèrement en cas d’un nombre total qui n’est pas divisible par 4 ou 5).
La méthode des effectifs égaux peut être utile dans le cas où l’on souhaite avoir une mise en classe comparable entre plusieurs cartes. Mais elle ne garantit en aucun cas de séparer des valeurs semblables. Dans le cas de la série de valeurs que nous avons déjà vu:
| 4,9 | 4,95 | 4,98 | 5,01 | 5,47 | 5,48 |
la méthode des effectifs égaux pourrait sélectionner la médiane (qui fait partie des quartiles), et du coup il y aurait une limite de 5,0. Ainsi, les valeurs semblables de 4,98 et 5,01 se retrouveraient dans une classe différente.
1.9.4.3. Méthode des amplitudes égales#
La méthode des amplitudes égales, appelée aussi méthode des intervalles égaux, divise l’étendue de la série statistique en plages de taille égale. Ainsi, sachant que la proportion de jeunes des communes suisses variait en 2022 entre 2,4% et 33,3%, on pourrait faire des limites simplement à 5%, 10%, 15%, 20%, 25% et 30%, donnant ainsi 7 classes.
Cette méthode donne des résultats satisfaisant uniquement dans certains cas où la série statistique suit une distribution uniforme. Elle ne garantit en aucun cas que le critère de séparation des valeurs semblables est respectée.
Pour illustrer le problème, nous pouvons regarder le nombre de communes pour les classes sur la proportion de jeunes:
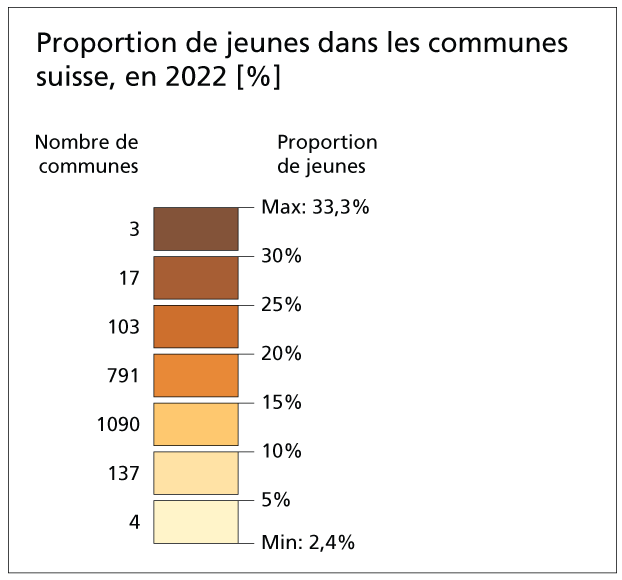
Avec cette mise en classe, plus de 85% des communes se trouvent dans uniquement 2 classes sur 7 classes. Une telle carte ne serait pas très informative.
Dans la pratique, la méthode des amplitudes égales n’est utile que très rarement. Cependant, étant sa simplicité, elle est souvent utilisée par des personnes qui ne sont pas familières avec la théorie de la cartographie.
1.9.4.4. Méthode par progression géométrique#
La méthode par progression géométrique est utilisée dans certains cas où la distribution est très dissymétrique. Les écarts entre les limites de classes augmentent ou diminuent au fur et à mesure.
Cette méthode nécessite le calcul d’un paramètre \(r\) qui est calculée comme suit:
où \(k\) correspond au nombre de classes. Le logarithme est en base 10.
Ensuite, les limites de classes peuvent être calculées comme suit:
pour une distribution dissymétrique à gauche:
\(L_1 = X_{min} \cdot r\)
\(L_2 = X_{min} \cdot r^2\)
\(L_3 = X_{min} \cdot r^3\)
…
pour une distribution dissymétrique à droite:
\(L_1 = X_{min} + X_{max} - X_{min} \cdot r\)
\(L_2 = X_{min} + X_{max} - X_{min} \cdot r^2\)
\(L_3 = X_{min} + X_{max} - X_{min} \cdot r^3\)
…
Il faut encore noter que cette méthode ne va pas garantir de garder ensemble des valeurs semblables, et la distribution est considérablement transformée.
1.9.4.5. Méthode de Jenks#
La méthode de Jenks est une méthode calculée à l’aide d’un algorithme informatique et qui se base sur le principe de grouper les valeurs semblables dans la même classe, et de séparer des valeurs différentes. Mathématiquement, il s’agit d’un algorithme qui minimise la variance intra-groupe maximise la variance inter-groupes.
Ensemble avec la méthode des seuils naturels, c’est la seule méthode de mise en classe qui garantit que des valeurs semblables ne sont pas séparées en différentes classes. Pour cette raison, ces deux méthodes sont généralement à privilégier.
Au niveau du résultat, la méthode de Jenks est souvent semblable à la méthode des seuils naturels. La plupart des logiciels de cartographie et SIG proposent une mise en classe par Jenks.
1.9.4.6. Méthodes de clustering#
En statistiques, des méthodes similaires à ces méthodes de mise en classe existent. Elles sont connues sous le terme de clustering, ou parfois classification. Nous utilisons ici le terme de clustering, car le terme de classification est utilisé pour une autre classe de méthodes dans le domaine de l’apprentissage statistique.
Une méthode de clustering permet de regrouper des observations sur la base d’une ou plusieurs variables. La mise en classe en cartographie peut donc être considérée comme un cas spécial du clustering où le nombre de variable est 1.
De nombreuses méthodes de clustering existent. La méthode la plus connue est le k-means qui permet de créer \(k\) groupes. L’avantage de cette méthode est qu’elle est relativement simple à mettre en œuvre et la méthode est bien connue. Le désavantage est qu’on doit définir manuellement le nombre de classes.
La méthode de classification ascendante hiérarchique (qui est une méthode de clustering malgré le nom) est une alternative au k-means. Cette méthode crée en même temps une hiérarchie entre les groupes, ce qui permet de faire une décision du nombre de classes sur la base d’un critère clair et simple.
Les méthodes statistiques de clustering sont relativement peu utilisées en cartographie, mais il n’y a en principe aucune raison pour cela. Ces méthodes respectent très bien le principe de regroupement de valeurs similaires dans la même classe. Le seul désavantage est que le nombre d’entités par classe peut être très déséquilibré. Le plus simple est d’essayer une des méthodes de clustering, et d’utiliser une des méthodes issues de la cartographie si la taille des classes est trop déséquilibrée.
1.9.4.7. Calculer l’erreur de mise en classe#
Comme mentionné plus haut, la mise en classe introduit une distorsion ou une perte d’information en raison du regroupement des valeurs. Cette erreur peut évidemment affecter l’interprétation de la carte. On va donc essayer de la minimiser.
Pour quantifier cette erreur, il y a plusieurs approches qui existent. Une façon de l’estimer est la suivante:
Dans un premier temps, la moyenne des valeurs est calculée pour chaque classe. Ensuite, l’écart entre chaque valeur dans la classe avec cette moyenne est calculée. La moyenne de ces écarts donne l’erreur pour une classe. En fait, il s’agit simplement de l’écart moyen pour chaque classe, on peut évidemment calculer l’écart type qui mesure la même propriété.
Ensuite, nous pouvons simplement calculer la moyenne des écarts types pondérée par le nombre d’entités par classe. Une valeur plus petite représente une distorsion plus petite.
Ce calcul est relativement simple et permet de comparer deux mises en classes. Cependant, il faut être prudent dans la comparaison entre mises en classes avec un nombre de classes différentes, car plus il y a de classes, moins l’écart type sera grand.
Il faut encore noter qu’en statistiques, il y a des méthodes plus poussées pour estimer l’erreur de mise en classe. Ces méthodes sont évidemment tout à fait appropriées, mais une discussion dans les détails dépasse le cadre de ce cours.
1.9.4.8. Choix du nombre de classes#
Le nombre de classes doit être en principe quelque part entre 4 et 8 classes pour des raisons de perception.
La méthode des seuils naturels donne des indications sur combien de classes seraient appropriées sur la base des seuils observés.
La méthode des effectifs égaux ne peut être utilisée uniquement avec 4, 5 ou 6 classes.
Par ailleurs, des efforts ont été entrepris qui essaient de définir le nombre de classes sur la base du nombre d’entités représenté sur la carte. Parmi ces efforts, on trouve la règle de Huntsberger qui essaie d’estimer le nombre de classes \(k\) à l’aide d’une formule simple:
où \(N\) est le nombre d’entités géographiques.
Tandis qu’il est vrai qu’on peut faire potentiellement plus de classes avec un nombre important d’entités géographiques, ces tentatives ignorent toutes le fait que le nombre de classes doit nécessairement dépendre des données représentées. On peut donc au mieux utiliser ces formules comme première estimation du nombre de classes avant d’inspecter les données.
1.9.4.9. Discussion#
Dans la pratique, il faudra prendre la décision quelle méthode est la plus appropriée. Cette décision dépendra de plusieurs facteurs.
Si nous avons la possibilité de procéder à un clustering, p.ex. à l’aide de la méthode de la classification ascendante hiérarchique, c’est certainement une bonne décision. Ainsi, on aura aussi des indications sur le nombre de classes à retenir. Par contre, le clustering ne peut pas être appliqué dans tous les cas (p.ex. en raison du nombre d’entités très déséquilibré). En plus, il faut recourir à un logiciel statistique, ces méthodes n’étant généralement pas disponibles dans les logiciels de cartographie ou SIG.
Nous pouvons aussi toujours recourir à la méthode des seuils naturels qui permet également d’avoir une bonne idée sur le nombre de classes à retenir. Par contre, une telle mise en classe prend évidemment plus de temps qu’une méthode automatisée et qui est déjà disponible dans un logiciel.
Pour rapidement créer une carte avec une discrétisation raisonnable, nous pouvons utiliser la méthode de Jenks.
Il peut arriver qu’aucun seuil remarquable n’est présent dans les données. Dans ce cas, nous pouvons procéder à une mise en classe par quantiles, ou, si la distribution est uniforme, aux amplitudes égales. Si par contre la distribution est très dissymétrique, une mise en classe par progression géométrique peut être tentée.
Il peut aussi être une bonne idée de calculer l’erreur de mise en classe, et de choisir la méthode avec une petite erreur.
1.9.4.10. Après la mise en classe…#
Une fois que la mise en classe est terminée, nous pouvons créer sélectionner une palette de couleurs et créer la légende de la carte. Dans la légende, on essaiera de sélectionner des valeurs arrondies mais qui se trouvent évidemment entre les entités extrêmes des deux classes.
La figure ci-dessous donne une idée sur les points à considérer suite à la discrétisation:
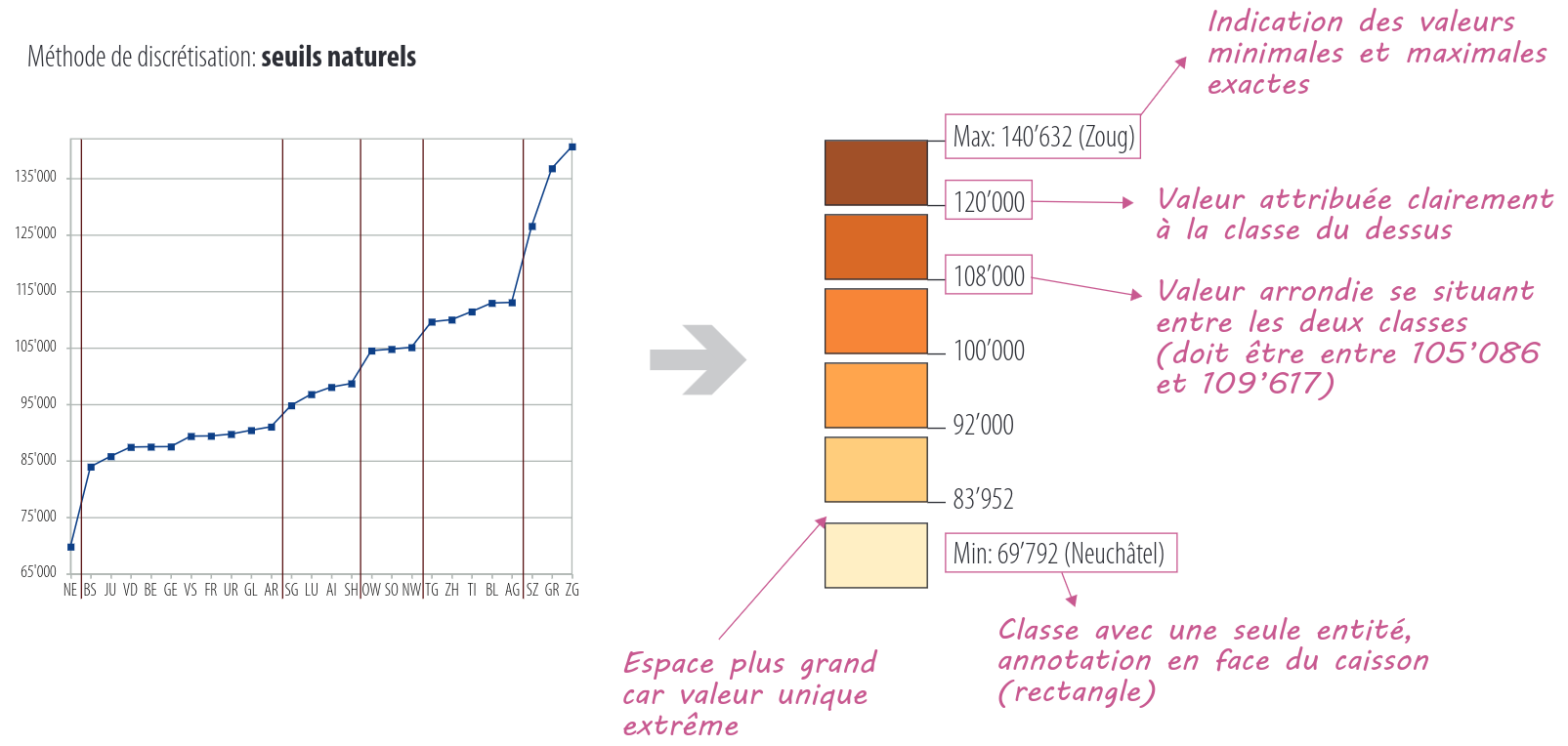
Les détails sur le choix de la couleur et de la mise en forme de la légende seront discutés plus tard. Pour le moment, on peut encore ajouter que les palettes de couleurs séquentielles de ColorBrewer consistent une bonne base pour le choix des couleurs.
