1.5. Généralisation cartographique#
La généralisation cartographique peut être définie comme le processus de réduction contrôlée de la quantité de détails sur la carte. On parle alors aussi du processus d’abstraction cartographique.
Au fur et à mesure que l’échelle de la carte diminue (une région plus grande est donc représentée sur la carte), plus il devient difficile de représenter tous les éléments sur la carte. À partir d’un certain moment, il y a une surcharge de la carte qui commence à apparaître. Un autre problème est que sur une carte, il faut souvent exagérer des éléments comme les routes. Exemple: si on mesure la largeur d’une autoroute sur une carte au 1:200’000 de Swisstopo comme celle en-dessous, on arrive à une largeur de 1 mm sur le papier. À cette échelle, cela représente 200 mètres. Or, un autoroute possède en vrai une largeur d’environ 30 mètres. Le problème arrive dans ce cas avec les éléments sur la carte qui se trouvent p.ex. à une distance de 50 mètres de l’autoroute. Sur la carte, ces éléments se retrouvent d’un coup sur l’autoroute; il faut donc les déplacer.
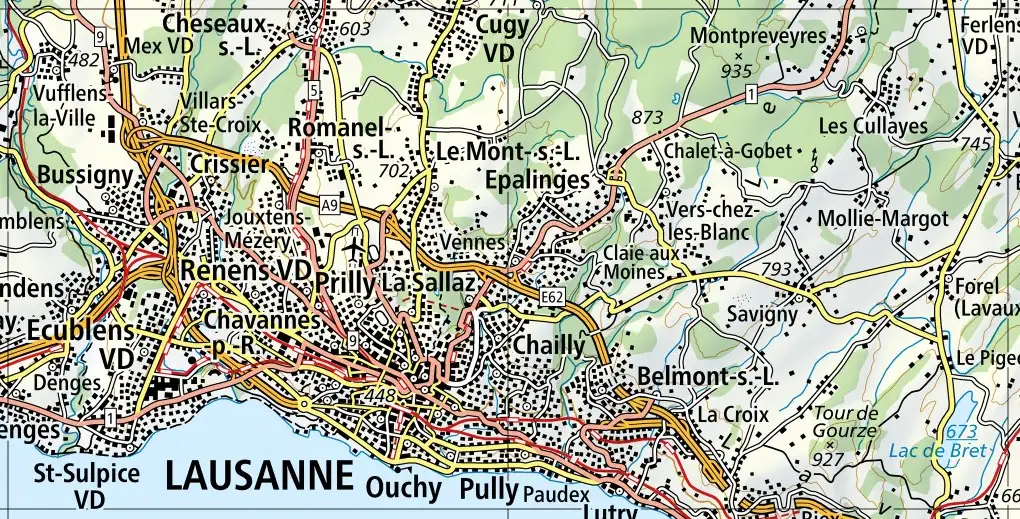Figure 1. Carte nationale à l’échelle 1:200’000. L’information est déjà bien généralisée, des routes manquent, le nombre de bâtiment a été réduit, uniquement les élément importants s’y trouvent. Source: Swisstopo
Afin de résoudre ce problème, la généralisation cartographique sélectionne et modifie l’information géométrique en fonction de l’échelle afin d’assurer la bonne lisibilité de la carte.
À l’aide de la généralisation, on va pouvoir garantir la lisibilité de la carte à toutes les échelles tout en évitant une surcharge d’informations. Le défi est de maintenir tout de même une précision spatiale ainsi qu’une bonne qualité esthétique.
Si on réduit simplement la carte, sans la généraliser, elle devient impossible. Ceci se voit sur la figure ci-dessous. La carte à l’échelle 1:25’000 (à droite) a été réduite une première fois de 50% (au milieu), et ensuite encore une fois de 50% (en bas à gauche). À gauche par dessus de la carte 1:25’000 réduite se trouve une carte à l’échelle 1:200’000 de la même région (donc agrandie). Notez l’importance des axes de communication et des cours d’eau sur la carte au 1:200’000, et la réduction et simplification des bâtiments et d’autres éléments:
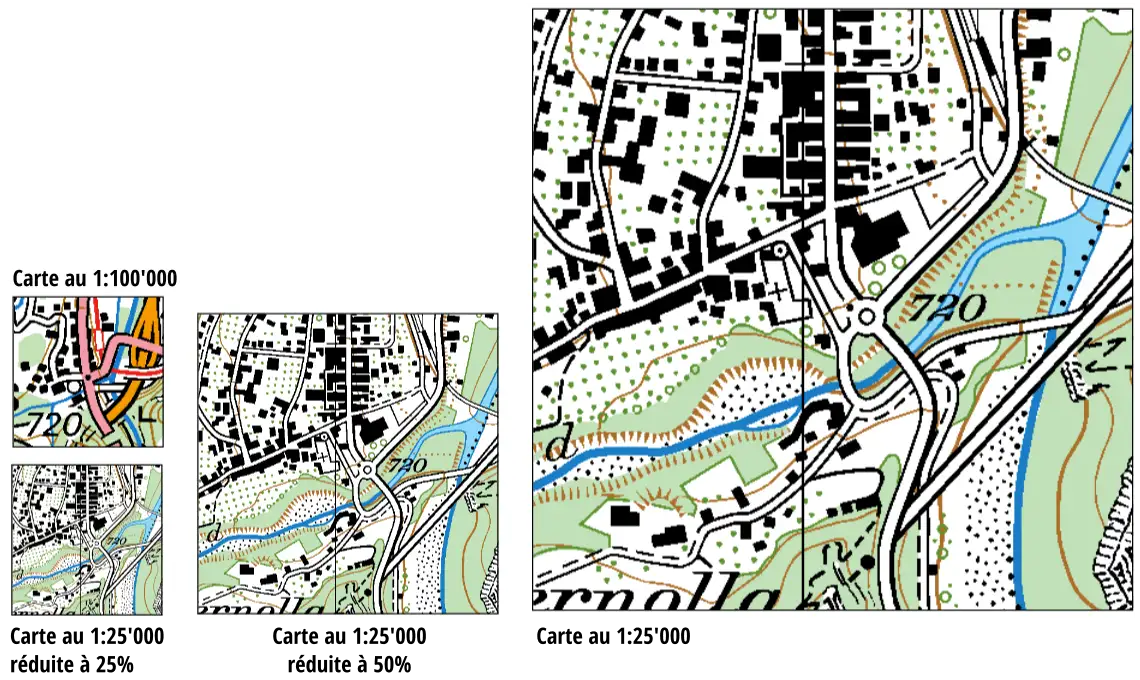Figure 2. Source: Swisstopo
Une considération importante pour la généralisation est également le but de la carte:
Dans une carte topographique, la précision de l’information géométrique doit être garantie aussi bien que possible. On va donc réduire l’information seulement autant que nécessaire.
Dans une carte routière, on va typiquement mettre en évidence le réseau routier, ce qui se fait en exagérant les routes, en supprimant le moins de routes possibles (au moins parmi les routes carrossables). Par contre, les éléments qui ne servent pas directement au but de trouver le chemin à l’aide de la carte pourront être enlevés. Ainsi, on n’aura pas besoin de tous les bâtiments, cours d’eau etc.
Le but premier d’une carte thématique est de transmettre une information ciblée sur un phénomène très précis. On pourra donc bien réduire la complexité de l’information géométrique et focaliser uniquement sur ce qui est vraiment essentiel. La précision géométrique n’est pas très importante dans une carte thématique.
1.5.1. Opérateurs de généralisation#
Plusieurs opérateurs et techniques sont utilisées pour la généralisation cartographique. La figure ci-dessous donne un aperçu de quelques-uns des opérateurs les plus utilisés:
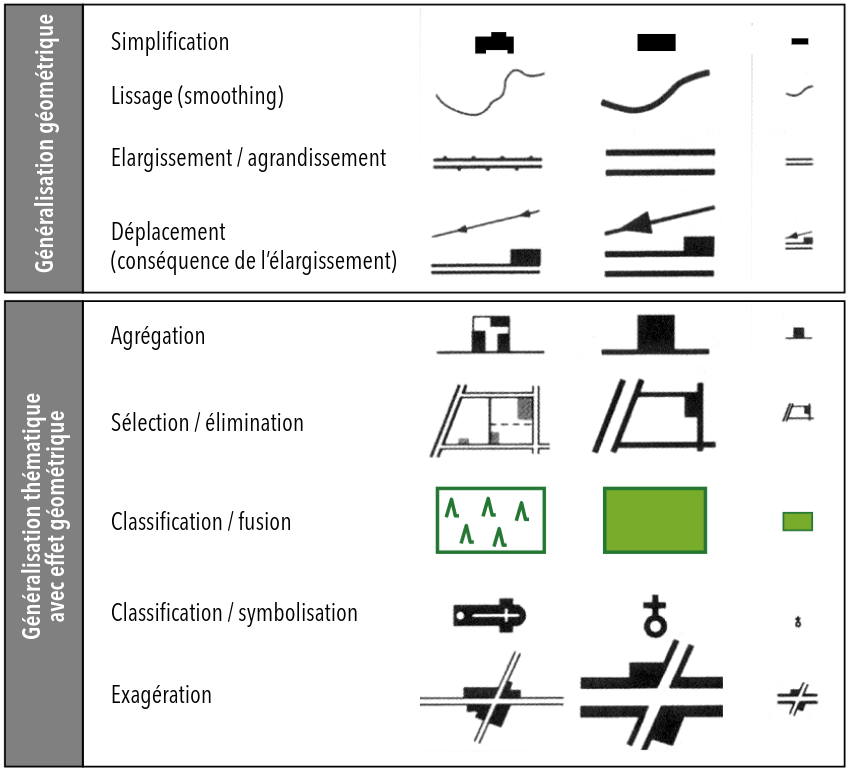Figure 3. Les opérateurs de généralisation les plus importants.
La sélection est un opérateur essentiel. Il s’agit de décider quels éléments et détails il faut inclure ou exclure sur la carte, et ceci en fonction de leur pertinence et importance par rapport à l’échelle et l’objectif de la carte. La sélection fait p.ex. qu’on va omettre certaines routes, ou que certaines localités sont omises.
La simplification est un autre opérateur de généralisation important. Cette technique permet de réduire la complexité d’un élément. Le but est de réduire les détails inutiles d’une géométrie, tout en conservant la forme de base. Ainsi, on peut simplifier un bâtiment en rectangle, ou un cours d’eau pourrait être plus moins sinueux.
Le lissage est un opérateur qui s’applique essentiellement aux géométries linéaires et qui est très similaire à la simplification. Cependant, le but du lissage est de rendre les géométries moins irrégulières (plus lisses…).
L’agrégation regroupe plusieurs éléments proches du même type en une seule forme simplifiée. Par exemple, un ensemble de maisons peut être représenté comme une seule géométrie.1
L’exagération augmente la taille de certains éléments importants et ainsni les rendre plus visibles.
Le déplacement est une conséquence directe de l’exagération. Si un élément est exagéré (p.ex. une route), les éléments qui se trouve en réalité à côté et doivent être déplacés pour ne pas se retrouver sur l’élément exagéré. Parfois, le déplacement d’un élément nécessite le déplacement d’un autre, menant parfois à une agrégation entre plusieurs éléments de même nature (p.ex. regroupement de plusieurs maisons.)
La fusion est la transformation d’un élément d’une dimension à une autre. Ainsi, un groupe d’arbre (ensemble de points) peut devenir une forêt (un polygone). Mais la fusion comprend aussi la transformation d’un polygone de rivière d’une carte à grande échelle en ligne sur une carte à une échelle plus petite. Ou à l’inverse la transformation d’un groupe de bâtiments en point représentant un lieu, ou en polygone représentant une zone habitée.
La symbolisation va remplacer la géométrie d’un élément par un symbole, p.ex. les différents éléments d’un aéroport (bâtiments, pistes, etc.) en un seul symbole d’un avion.
La fusion et la symbolisation sont parfois similaires, comme p.ex. pour la transformation d’un groupe de bâtiments en point pour symboliser un lieu. La différence est que pour la fusion, on va habituellement considérer des éléments du même type.
1.5.2. Généralisation d’éléments non vectoriels#
La généralisation comme nous l’avons vue jusqu’ici s’applique à des géométries vectorielles.
Par contre, même d’autres éléments qui sont typiquement représentés sous forme d’image raster doivent suivant comment être généralisés. Ainsi, le dessin des rochers (faits à la main!) doit aussi être adapté à l’échelle de la carte:
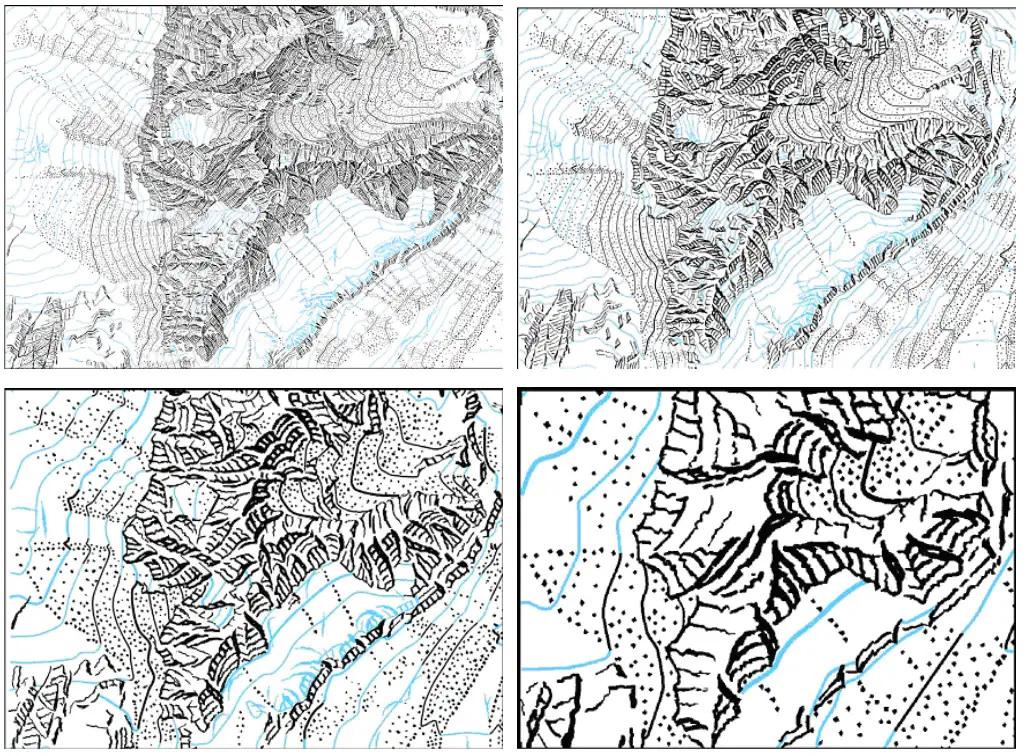
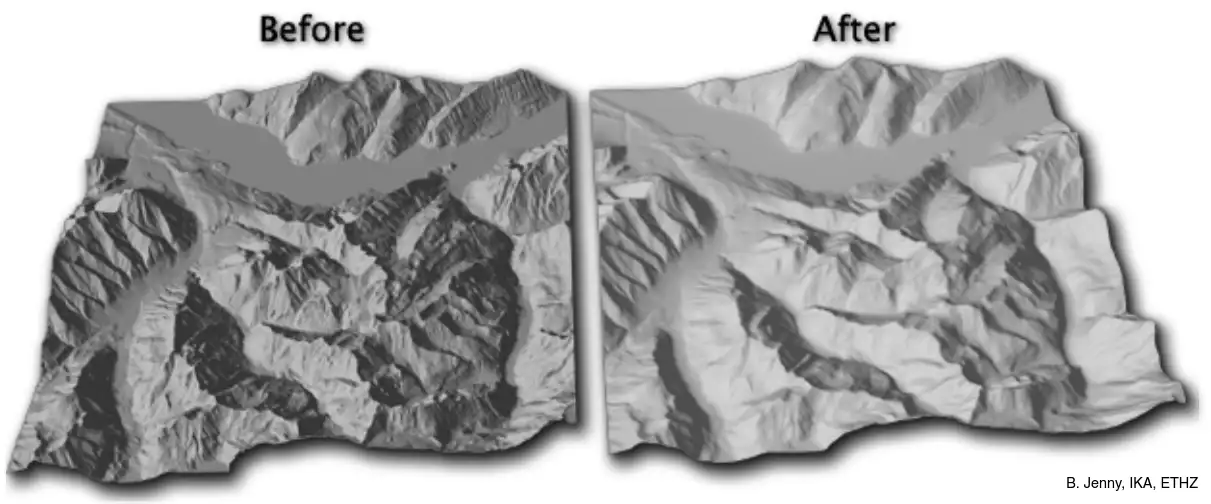
C’est aussi le cas du relief ombré, où le relief à droite sur la figure ci-dessous est plus généralisé que celui à gauche:
1.5.3. Résumé#
Il est important d’adapter le niveau de généralisation de la carte:
en fonction de l’échelle de la carte
en fonction du but de la carte
en fonction du public cible (pour un public large, il faut réduire l’information davantage que pour un public de spécialistes)
en fonction du support utilisé (p.ex. une carte à la télé doit être généralisée davantage qu’une carte dans un rapport scientifique, car la qualité de l’image et la durée que le lecteur regarde la carte ne sont pas pareils)
Attention aussi d’utiliser le même niveau de généralisation pour toutes les couches. Sinon, il peut arriver que vous trouvez la ligne du train dans un lac, ou l’autoroute qui passe à travers des bâtiements. Pour beaucoup de couches sont disponibles à des niveaux de généralisation différents. Très souvent, c’est l’échelle d’utilisation prévue sera mentionnée pour un jeu de données.
Ainsi, consultez p.ex. le site Web NaturalEarth. Ce site distribue des couches vectorielles et raster pour l’ensemble de la Terre. Les données sont disponibles à trois échelle différentes (voir dans la section “Downloads”).
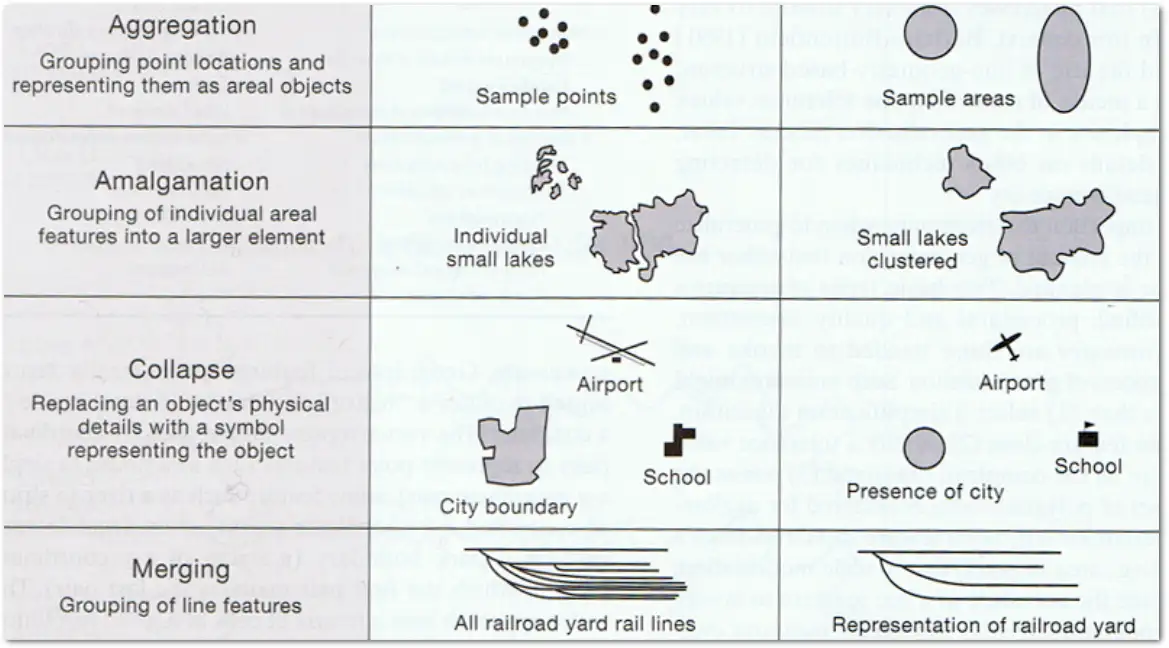
1 La terminologie des opérateurs peut différer d'un auteur à l'autre. Ainsi, certains distinguent p.ex. l'agrégation de l'amalgamation. Dans ce cas, l'agrégation correspond à l'opérateur de fusion, et l'amalgamation correspond à notre opérateur d'agrégation. La figure ci-dessous donne quelques exemples d'une terminologie un peu différente. Cependant, tous les opérateurs se retrouvent d'une manière ou d'une autre dans chaque terminologie. Dans ce livre, nous utilisons généralement la terminologie définie dans la figure 3 ci-dessus.
