1.3.2. Carte en symboles proportionnels#
Une carte en symboles proportionnels contient les régions en arrière plan, avec des symboles à taille variable par dessus. Ces symboles sont généralement des cercles ou des carrées, mais parfois on voit aussi d’autres formes.
Voici un exemple d’une carte en symboles proportionnels:
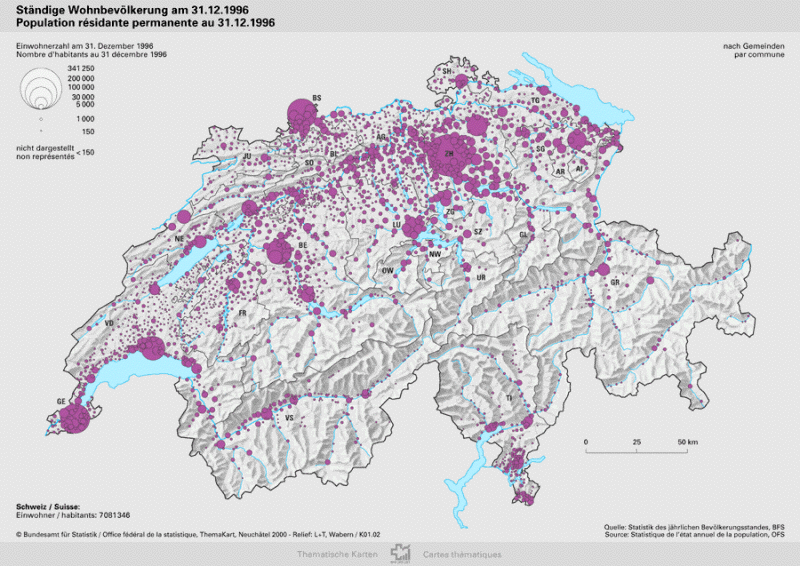
Source: Office fédéral de la statistique
La surface du symbole est proportionnelle à la valeur représentée (et non pas le rayon ou le diamètre!).
Important: La carte en symboles proportionnels permet de représenter uniquement des données absolues comme des nombres, effectifs, quantités et autres valeurs additives. Elle ne permet pas de représenter des données relatives (proportions, taux, densités etc.). Elle est donc complémentaire à la carte choroplèthe qui ne permet pas de représenter des valeurs absolues, mais seulement des valeurs relatives.
Données absolues vs données relatives. En cartographie, on distingue les données ou valeurs absolues des données ou valeurs relatives pour déterminer comment les données peuvent être représentées. Mais il ne s'agit pas de valeurs absolues dans le sens mathématique.
Dans le sens de la cartographie, les données absolues correspondent à des nombres typiquement entiers, des effectifs et autres quantités additives, c'est-à-dire des données que l'on arrive à compter.
En opposition, les données relatives sont aussi des données quantitatives, mais correspondent à des valeurs calculées tels que les proportions, pourcentages, taux ou densités. Il s'agit quasi exclusivement de nombre à décimales.
1.3.2.1. Taille des symboles#
Un des défis d’une carte en symboles proportionnels est de bien dimensionner les symboles. C’est au cartographe de définir une taille idéale en agrandissant ou réduissant l’ensemble des symboles. En effet, la taille des symboles est calculée comme suit:
où \(s\) est le rayon du symbole dans le cas d’un rond, et la taille dans le cas d’un carré. \(N\) est la valeur à représenter. La puissance 0.5 n’est rien d’autre que la racine carrée. \(k\) est un facteur de mise à l’échelle pour s’assurer que les symboles sont de manière globale pas trop grands ou trop petits. Le cartographe devra donc trouver une valeur appropriée pour ce facteur \(k\). \(k\) est évidemment la même valeur pour tous les symboles sur une même carte.
Il peut arriver que les symboles sur une telle carte se chevauchent. Ce n’est pas un problème tant que les différents symboles et leur taille peuvent toujours être reconnus sans problème.
On va évidemment éviter un chevauchement trop important, mais en même temps il faut aussi s’assurer que les petits symboles sont toujours visibles sans problème. Il faut donc trouver un bon équilibre au niveau de la taille.
De manière générale, lorsqu’il y a superposition, les petits symboles doivent toujours se trouver par dessus les grands.
Généralement, on utilise des symboles remplis à l’intérieur, avec un contour fin en blanc ou en noir. Dans quelques rares cas, on voit aussi des symboles dont uniquement le contour est présent; ces cartes sont par contre souvent moins bien lisibles:
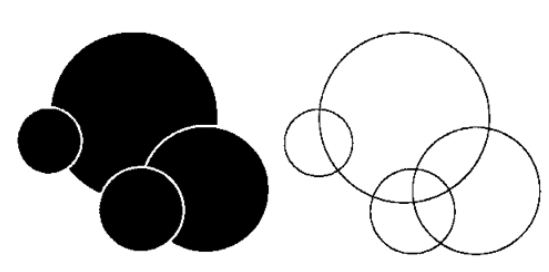
Parfois, il arrive qu’il y a un symbole énorme, et les autres beaucoup plus petits. Dans ce cas, il peut faire du sens de représenter uniquement le contour du symbole énorme, et les autres normalement avec un remplissage. Cette technique est cependant réservée aux cas extrêmes.
Si quelques symboles sont trop petits, on peut les agrandir à une taille minimale. Cependant, il faut que ce n’est utilisé uniquement pour un petit nombre de symboles, et il faudra également l’indiquer dans la légende.
1.3.2.2. Les problèmes de perception#
L’estimation de la taille des symboles n’est pas toujours évidente pour l’humain. Avec les cerlces, il peut y avoir un phénomène de perception qui fait que la plupart des personnes sous-estiment la taille des cercles. Ce phénomène a été observée par J.J. Flannery en 1956, dans sa thèse «The graduated circle; a description, analysis and evaluation of a quantitative map symbol» (thèse de doctorat faite au Departement of Geography de l’University of Wisconsin à Madison).
Dans ce travail remarquable il avait constaté cette sous-estimation typique de la taille des symboles arrivait avec les cercles (elle n’arrive pas avec des carrés!). Il avait également déterminer une taille correcte en terme de perception. Au lieu de calculer la taille du rayon d’un cercle de la manière classique correspondant à la formule déjà introduit en haut:
(ou \(s\) a été remplacé par \(r\) vu que ça s’applique uniquement aux cercles)
il faut calculer le rayont de la manière suivante:
C’est donc la puissance qui change, il ne faut pas prendre la racine carrée, mais une valeur légèrement différente.
Cette correction est appelée la correction de Flannery. La figure ci-dessous donne une idée sur l’effet de cette correction:
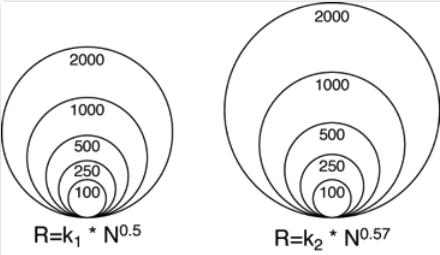
Si nous faisons une carte en symboles proportionnels avec des cercles, il est généralement conseillé d’appliquer cette correction de Flannery. Une autre option est de choisir des carrés comme symboles. Dans ce cas, le phénèmone de sous-estimation des tailles ne survient pas.
