1.9.3. Distribution statistique#
Une variable est considérée ici comme étant une série de valeurs. On parlera aussi d’une série statistique. En conséquence, on parlera de la distribution statistique de la variable.
Des exemples d’une telle série statistique pourraient être:
le nombre d’habitants par commune vaudoise
la proportion de jeunes par canton suisse
la concentration en CO2 aux stations de mesure du canton de Vaud
La caractérisation d’une série de valeurs se fait essentiellement à l’aide de mesures de position, de dispersion et avec l’histogramme de fréquence.
1.9.3.1. Les mesures de position#
Les mesures de position permettent de définir une série statistique à l’aide de quelques valeurs simples. On parle aussi de paramètre ou d’indicateur de position.
Une mesure de position peut être un indicateur de tendance centrale, ou une valeur décentrée.
Les valeurs minimum et maximum.
La moyenne \(\bar x\). La moyenne se calcule simplement en calculant la somme des valeurs et en divisant par le nombre d’observations:
\[\bar x = \frac{1}{N} \cdot \sum_{i=1}^N X_i\]où \(X_i\) est la valeur de la \(i\)ème entité sur un total de \(N\) entités.
La moyenne peut être utilisée pour estimer la valeur centrale d’une distribution.
Il faut encore noter que la moyenne ne peut en principe pas être calculée sur des valeurs relatives telles que des pourcentages si les entités ont des tailles différentes. P.ex. une commune A possède 10’000 habitants, dont 2’000 jeunes. Elle a donc une proportion de jeunes de 20%. Une commune B a seulement 100 habitants, dont 10 jeunes, donc une proportion de 10% de jeunes. Une moyenne simple donne \(10 + 20 = 15\). Or, au total il y a 2’010 jeunes sur un total de 12’000 habitant, ce qui correspond à 16.75%.
La moyenne est par ailleurs aussi sensible aux valeurs extrêmes. Par exemple la moyenne des valeurs 2, 2, 4, 100’000 est 25’002, tandis que la moyenne pour les 3 premières valeurs est seulement \(2 \frac{2}{3}\). Une seule valeur peut donc sensiblement influencer la moyenne.
La médiane est une autre estimation pour la valeur centrale. Elle sépare la série statistique en deux parties égales. Donc p.ex. avec 100 valeurs, la médiane correspond à la valeur où 50 valeurs sont plus petites, et 50 valeurs plus grandes. La médiane est une estimation plus robuste que la moyenne, car elle ne se laisse que très peu par des valeurs extrêmes.
Le mode est une autre valeur permettant de caractériser une distribution statistique. Il s’agit de la valeur dominante, c’est-à-dire de la valeur la plus fréquente. Une distribution peut avoir un seul mode, on dit alors qu’elle est mono-modale. Ou elle peut avoir plusieurs modes; elle est multi-modale dans ce cas.
Les quartiles et les déciles. Ce sont deux mesures qui sont des variantes des percentiles (aussi appelées les quantiles).
Le \(n\)ième percentile (où \(n\) est une valeur entre 1 et 99) correspond à la valeur qui est plus grande que \(n\)% des valeurs dans la série statistique, et en conséquence plus petite que \(100 - n\)% des valeurs. Ainsi, la valeur du 20ème percentile est plus grande que 20% des observations dans une série statistique. Pour le calcul des percentiles, il y a évidemment le problème comment définir la valeur si la série statistique ne possède pas exactement 100 valeurs, mais par exemple 17 valeurs. Plusieurs façons de calculer existent pour ce problème, mais qui dépassent le cadre de cette courte présentation.
Les quartiles correspondent aux 25ème, 50ème et 75ème percentiles. On parle alors du 1er quartile (25ème percentile), 2ème quartile (50ème percentile) et 3ème quartile (75ème percentile).
Attention de ne pas confondre quartile et quantile. Quantile est un synonyme de percentile.
Par ailleurs le 50ème percentile (2ème quartile) correspond par définition à la médiane.
Les déciles correspondent aux 10ème, 20ème, 30ème, …, 90ème percentiles. Le 5ème décile correspond au 2ème quartile et à la médiane.
1.9.3.2. Les mesures de dispersion#
Les mesures de dispersion, appelées aussi paramètres ou indicateurs de dispersion, permettent d’évaluer la variabilité des valeurs d’une série statistique.
Pour comprendre l’idée, voici deux exemples différents de séries statistiques:
A: 4, 4, 5, 5, 6, 6
B: 1, 1, 5, 5, 9, 9
La moyenne et la médiane des séries A et B sont identiques, à savoir 5. Par contre, les valeurs de la série A sont toutes entre 4 et 6, tandis que pour la série B, elles varient entre 1 et 9. Nous pouvons évaluer cette différence notamment avec une mesure de dispersion.
L’étendue est une telle mesure de dispersion, même si elle est très simple:
Un autre indicateur de dispersion est l’écart interquartile qui est la différence entre le 1er et 3ème quartile.
L’écart moyen est un indicateur de dispersion facile à comprendre et à calculer, mais qui est peu utilisé. Il s’agit de la moyenne des écarts absolus à la moyenne, ou sous forme de formule:
Un autre indicateur de dispersion qui est calculé de manière similaire est l’écart type. Au lieu de prendre la valeur absolue des écarts, le carré des écarts est calculé, et à la fin pour “compenser” on prend la racine carrée. Le signe habituel pour l’écart type est \(\sigma\):
L’écart type est bien plus important en statistiques que l’écart moyen, en raison de ses propriétés mathématiques. Par ailleurs, l’écart moyen n’est jamais plus grand que l’écart type. L’écart type est aussi l’indicateur de dispersion le plus important en cartographie.
Le deuxième paramètre de dispersion important est la variance qui est simplement le carré de l’écart type:
1.9.3.3. L’histogramme de fréquence#
L’histogramme de fréquence est la représentation graphique montrant la répartition empirique d’une série statistique. L’axe des x représente les valeurs possibles de la variable, et l’axe des y le nombre d’observations pour une plage représentée par une barre. Voici l’exemple de l’histogramme de fréquence de la proportion de jeunes dans les communes suisses:
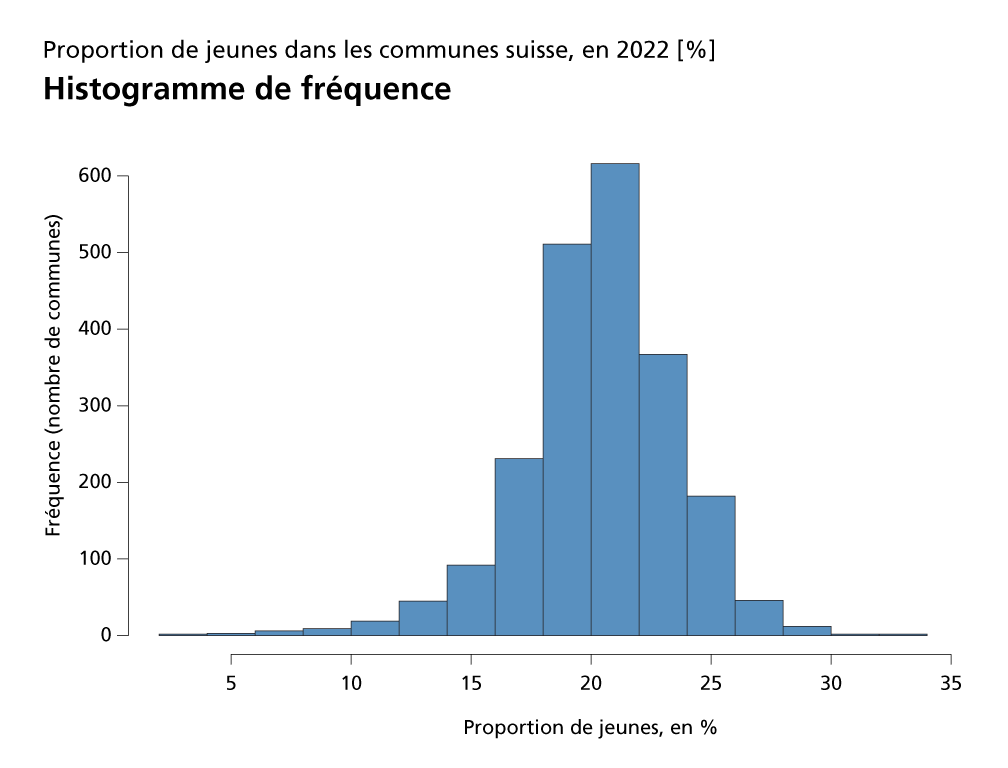
Un tel histogramme peut prendre des formes très variées selon la nature des données. Voici l’exemple de l’histogramme de fréquence du nombre d’habitants par commune suisse:
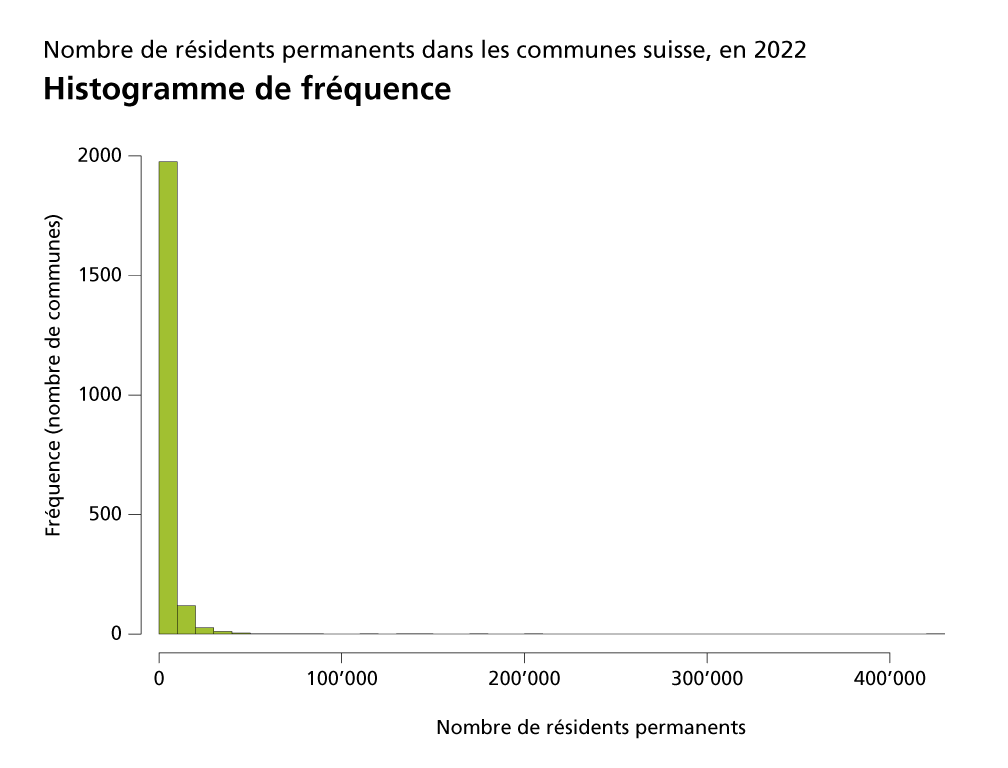
Il y a donc en Suisse un grand nombre de petites communes, et seulement quelques-unes (à peine visible dans l’histogramme) de 50’000 ou plus d’habitants.
Ces histogrammes de fréquence empiriques (c’est-à-dire sur la base de valeurs observées) peuvent être remplacés par des courbes théoriques. Il faut s’imaginer que la largeur des barres est réduite jusqu’à une largeur de 0, et les barres deviennent une aire avec une courbe. Certaines de ces courbes peuvent être représentées à l’aide d’une équation; on parle alors d’une courbe de distribution. La fréquence est alors remplacée par la probabilité que la variable prend une certaine valeur.
La courbe de distribution représente alors la distribution statistique. Certaines distributions statistiques sont très caractéristiques et répandues. La distribution la plus connue est certainement la distribution normale, aussi appelée distribution gaussienne. La courbe de distribution (théorique du coup) représente une jolie forme de “cloche”:
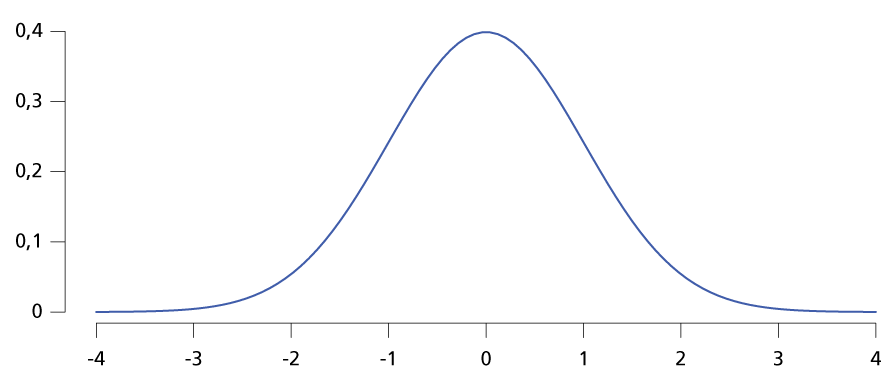
La courbe de la distribution gaussienne est symétrique. La valeur de 0 dans cette figure représente la moyenne et la médiane qui sont égales dans une distribution normale. Les valeurs de l’axe des x représentent les écarts types (les données de la figure ci-dessus ont donc un écart type de 1). Le point d’inflexion de la courbe se trouve à -1 resp. +1 écart type.
1.9.3.4. Distributions statistiques#
On distingue plusieurs distributions statistiques que l’on peut entre autres caractériser à l’aide de la courbe de distribution (resp. l’histogramme de fréquence), ainsi qu’à l’aide de quelques indicateurs statistiques simples comme la moyenne ou la médiane.
Les distributions les plus importantes en cartographie sont les suivantes:
La distribution normale dont nous avons déjà vu la courbe symétrique sous forme de cloche.
Une distribution dissymétrique où la courbe “penche” soit à gauche, soit à droite:
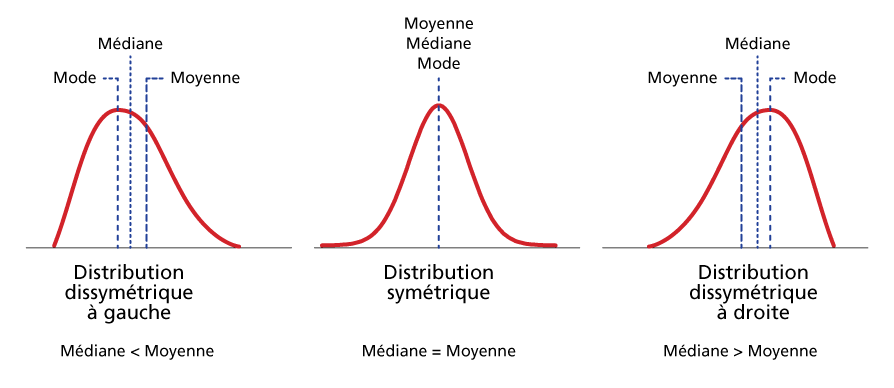
Ce qui est caractéristique avec une distribution dissymétrique est que la médiane n’est pas égale à la moyenne.
L’histogramme de fréquence du nombre d’habitants par commune ci-dessus est un exemple classique d’une distribution (très) dissymétrique.
Dans le cas d’une distribution uniforme, toutes les valeurs ont la même probabilité, l’histogramme de fréquence est en conséquence très équilibré:
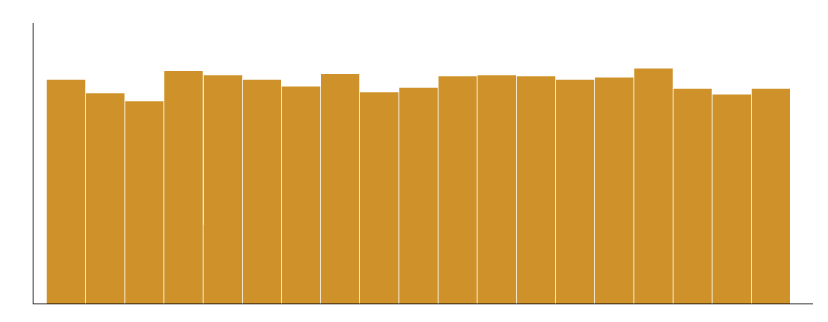
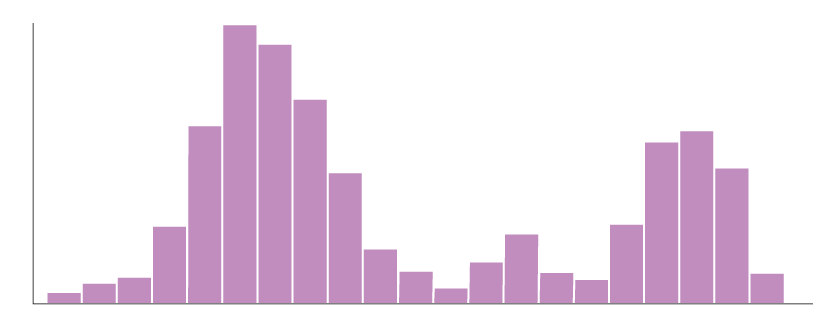
Parfois, une distribution possède plusieurs modes, on parle alors d’une distribution multi-modale, dont voici un histogramme de fréquence:
En statistiques, on distingue nettement plus de distributions, et ceci de manière beaucoup plus fine. Mais pour la mise en classe en cartographie, cette catégorisation suffit généralement.
Avec ces quelques connaissances statistiques de base, nous pouvons maintenant regarder les méthodes de mise en classe les plus utilisées en cartographie.
